Matematikastudycenter.com_ 2021 Menentukan daerah dua lingkaran dibatasi dua garis singgung lingkaran. Standar yang diperlukan antara lain aturan pythagoras, menentukan panjang garis singgung persekutuan luar, menentukan sudut dari sinus atau cosinus segitiga, luas trapesium, dan luas juring dari suatu lingkaran.
Soal
Lingkaran C1 dan C2 masing-masing berjari-jari 1 dan 7, dan jarak kedua pusat lingkaran tersebut 12. Jika PQ dan
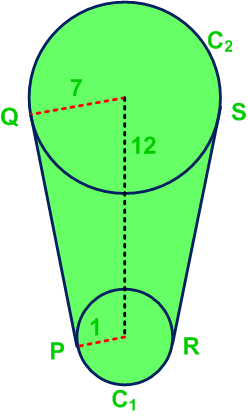
RS adalah garis singgung persekutuan luar kedua lingkaran tersebut maka luas daerah yang diarsir: (UMPTN Matematika IPA 1994)
A. 33π + 8 √3
B. 33π + 16 √3
C. 33π + 24 √3
D. 33π + 32 √3
E. 33π + 48 √3
.Pembahasan
Perhatikan gambar berikut terlebih dahulu.
Sebelum masuk ke luas, terlebih dahulu ditentukan panjang garis singgung PQ, besar sudut beta dan besar sudut alpha pada gambar di bawah.
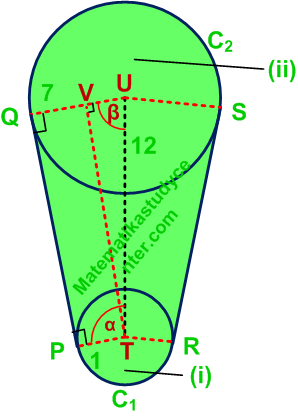
Panjang garis singgung PQ
PQ = √(122 − (7 -1 )2)
PQ = √(144 − 36)
PQ = √108 = 6√3Garis PQ ini berlaku sebagai tinggi untuk trapesium PQUT.
Besar sudut beta dan α
Dari segitiga siku-siku TVU di mana TU = 12, VU = 6
cos β = VU/TU = 6/12 = 1/2
β = 60°Dari gambar terlihat bahwa besar sudut alpha
α = 90° + 30° = 120°
Luas daerah yang di arsir adalah Luas dua kali luas trapesium PQTU kemudian ditambah luas daerah (i) ditambah dengan luas daerah (ii)
Luas trapesium PQTU
= (jumlah dua sisi sejajar)x t/2
= (1 + 7) x 6√3 /2
= 8 (3√3)
= 24√3 satuan luas
Luas daerah (i) gunakan mencari luas juring suatu lingkaran
Luas = (360° – 2α)/360° x πr12
= (360° – 240°)/360° x π(1)2
= (1/3)π
Luas daerah (ii)
Luas = (360° – 2β)/360° x πr22
= (360° – 120°)/360° x π(7)2
= (2/3)π x 49
= 98/3 πLuas seluruhnya
= 2xluas trapesium PQUT + L(i) + L(ii)
= 2×24√3 + (1/3)π + (98/3)π = 48√3 + (99/3)π
= 48√3 + 33π
Jawaban: E.
