Matematikastudycenter – Contoh soal pembahasan luas daerah dan volume benda putar, ujian nasional UN matematika SMA terkait skl / kisi-kisi dengan indikator : Menghitung luas daerah dan volume benda putar dengan menggunakan integral.
Berikut contoh soal-soal UN materi Luas Daerah dan Volum Benda Putar:
1) UN Matematika SMA 2010 P04 – Kepulauan Riau
Luas daerah yang dibatasi oleh parabola y = 4x − x2, y = −2x + 8, dan sumbu Y adalah….
A. 4 2/3 satuan luas
B. 6 2/3 satuan luas
C. 12 2/3 satuan luas
D. 20 2/3 satuan luas
E. 30 2/3 satuan luas
2) UN 2010 Yogyakarta
Luas daerah di kuadran I yang dibatasi oleh oleh kurva y = x3, y = x, x = 0 dan garis x = 2 adalah….
A. 2 1/4 satuan luas
B. 2 1/2 satuan luas
C. 3 1/4 satuan luas
D. 3 1/2 satuan luas
E. 4 1/4 satuan luas
3) UN Matematika SMA IPA P04 2010 Kepulauan Riau
Daerah yang dibatasi oleh kurva y = 4 − x2, sumbu X, sumbu Y dan garis x = 1. Volume benda putar yang terjadi jika daerah tersebut diputar mengelilingi sumbu X adalah…
A. 12 8/15 π satuan volum
B. 12 8/12 π satuan volum
C. 13 8/15 π satuan volum
D. 13 8/12 π satuan volum
E. 14 π satuan volum
4) UN Matematika SMA 2010-Yogyakarta
Volume benda putar yang terjadi bila daerah yang dibatasi oleh kurva y = x2 dan daerah y = √x diputar 360° mengelilingi sumbu X adalah….
A. 3/10 π satuan volum
B. 5/10 π satuan volum
C. 1/3 π satuan volum
D. 10/3 π satuan volum
E. 2π satuan volum
5) UN Matematika SMA 2010 P37 Kepulauan Riau
Volume benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = 2x − x2 dan y = 2 − x diputar mengelilingi sumbu X sejauh 360° adalah….
A. 1/5 π satuan volum
B. 2/5 π satuan volum
C. 3/5 π satuan volum
D. 4/5 π satuan volum
E. π satuan volum
6) UN 2011 Paket 12 Yogyakarta
Volume benda putar jika daerah yang dibatasi oleh kurva y = x2, garis y = 2x di kuadran I diputar 360° terhadap sumbu X adalah….
A. 20/15 π satuan volum
B. 30/15 π satuan volum
C. 54/15 π satuan volum
D. 64/15 π satuan volum
E. 144/15 π satuan volum
Pembahasan Soal Nomor 2
Sketsa grafik yang dibentuk oleh kedua fungsi, cari titik potong y = x3 dan y = x
Titik potong :
x3 = x
x3 − x = 0
x(x2 − 1) = 0
x(x − 1)(x + 1) = 0
x = 0 v x = 1 v x = − 1
Karena dibatasi juga oleh garis x = 0, maka titik potong yang digunakan adalah 0 dan 1 saja. Berikut sketsa kasar grafiknya:

Dari sketsa grafik terlihat dua area yang harus dicari luasnya, area pertama dibatasi oleh 0 dan 1, area kedua dibatasi oleh 1 dan 2 selengkapnya perhitungan mencari luasnya sebagai berikut:
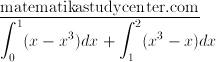
Kita hitung secara terpisah saja untuk mengurangi resiko kesalahan perhitungan akibat kurangnya ketelitian
Luas area pertama
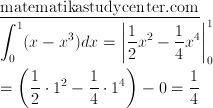
Luas area kedua
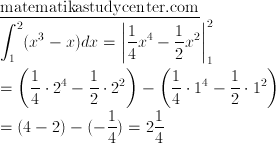
Jumlahkan
2 1/4 + 1/4 = 2 1/2 satuan luas
Pembahasan Soal No. 5
Sketsa grafiknya. cari titik-titik potong:
2x − x2 = 2 − x
2x − x2 + x − 2 = 0
x2 − 3x + 2 = 0
(x − 2)(x−1) = 0
x = 2 v x = 1
Berikut sketsa kasar grafik selengkapnya
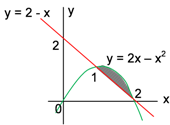
Waktunya berhitung:
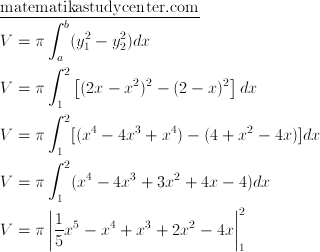
Eksekusi akhir